2021. 1. 10. 20:39ㆍCS231 Summary & 마음대로 해석

f(x,W) = Wx + b
Linear Classfier 에는 Algebraic Viewpoint, Bias Trick이 있다.
W = 가중치 = weights 라고 함

pixel을 낮췄을 경우, 사람의 경우는 인식이 쉽지만 컴퓨터가 인식하는게 달라진다.
Score가 낮아짐

2 by 2로 나누어서 오른쪽 차트 처럼 Algebraic Viewpoint F(x,W) = Wx+b 를 정렬
총 3총의 class (cat/ dog/ ship) 별로 template으로 나눔
Animal 별로 보면 색감으로 이제 인식할 것
예로들어 plane에는 파란색이 많은 걸로, deer은 초록색이 많은 걸로
하지만 car 같은 정체가 불분명 한 것은 classify가 어려울 것으로 예측됨
추가적으로, 1개의 template을 중보갛여 사용할 수는 없다.
Horse 경우, 2개의 머리를 가짐. 바라보는 Direction에 따라 달라져서 인식하기 어려워 진다는 것.

여러 픽셀을 살펴보기 위해 x축 한 픽셀, y축 한 픽셀 씩 뽑아서 봄

2 Dimensional로 보게 될 경우 위와 같은 lenear classifier 로 생성됨

위에는 Linear Classifier로 인식하기 힘든 경우의 케이스들을 설명

XOR function은 배울 수 없다.
그러하여 Geographic viewpoint가 더 실용적인지를 이야기 할 수 있다고 함.
아래는 Linear Classifier 의 3가지 View Points에 대해 정리


그럼 어떻게 제대로 된 W를 구할 수 있을까?

해야할 것!
1. loss funtion을 사용하여 W에 대한 좋은 값을 수량화 한다 .
2. loss function을 작게 만드는 W값을 구한다 (optimization = 최적화)

x 는 train set
y 는 정답
f 는 딥러닝 모델
L은 Loss function
Loss Function은 classfier가 좋은지 안좋은지를 알려준다
Loss 를 여기서 부정적으로 잃어지는 것으라고 생각하면 됨. loss = 손실
Negative loss functiond은 반대로 긍정적이게 reward function, profit funtion, utility funtion, fitness function 등으로 불림
위의 오른쪽 2번째 L i 공식은 Loss 구하는 공식
위의 오른쪽 3번째는 data set을 위한 Loss 공식?

SVM Loss

공식 대로 계산하여 보았을 때 Loss 값은 개구리가 가장 큼
마지막으로 Full data set에 대한 손실은 구한 값에서 /3 (class 수) 하여 평균값 구할 수 있음 = 5.27
- P49 Q1: What happens to the loss if the scores for the car image change a bit?
여기서 문제, 자동차 이미지에 대한 스코어가 조금이라도 변하면 loss 는 어떻게 되는가?
-> 이러한 경우, 현재 car에 대한 인식이 가장 좋으므로, 이후에 스코에 대한 변경을 주어도 loss score는 0에서 변함이 없다.
그것이 SVM Loss의 특징으로 볼 수 있다.
- P50 Q2: What are the min and max possible loss?
Min = 0 Correct category
Max= Infinite 무제한으로 될 수 있다. 특히나 correct category가 smaller loss score를 가질 경우에는 특히나!
- P51 Q3: If all the scores were random, what loss would we expect?
모든 score가 모두 random이라면 loss는 어떻게 예상하는가?
0은 나올 수 없음.
C-1 의 값을 나올 수 있다. (debugging technique으로 사용할 수 있다고함)

Sj - Sy1 이 부분이 모두 작은 숫자가 되는 것이고, 앞에 함수가 looping을 계속 함으로써...
- P52 Q4: What would happen if the sum were over all classes? (including i = y i )
총합 sum이 모두 correct category로
all score to be inflated by 1 (모두 1로 inflated되기 때문에 same preferencees가 적용 됨)
공식에 마지막 +1 해주는 걸로 이야기 하는 것 같음
* P53 Q5: What if the loss used a mean instead of a sum?
나오는 값을 똑같을거다.
monotonic process로서 ..
- P54 Q6: What if we used this loss instead?
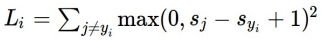
이러한 경우는 non linear way로 모든 것을 바꿀 것임.

Loss (L) 값이 0이 나온다면 이것은 특별한 일인가?
-> 아니다. 아래 2W값도 0으로 나오기 때문 (2W 는 W에 2를 곱해서 적용한 것)


여기서 질문, W와 2W의 값이 둘 다 같이 training data에서 나온다면 우린 어떠한 것을 골라야하는가 ?
-> 이럴 땐 Regularization 일반화 적용 = 1W = 2W 처럼 트레이닝 에러가 나오면 모델이 트레이닝 데이터에서 너무 잘 되는 것을 방지함.


Regularization = 람다 적용 (hyperpararmeter)
Regularization이란 Expressing Preferences 선호도 표시 !
위의 examples은 Regularizer로 불림
Regularizer의 사용 목적은,
1. adding additional term, 즉 에러가 일어난 트레이닝 결과 (not being distinguished status)에서 어떠한 선호값을 구하기 위해 사용
2. Overfitting을 피하기 위함. Overfitting은 교육 된 것은 잘 인식하지만 Unseen (보지못한) 자료에 대해서는 poor 한 결과값을 나오게 함. 이 부분에서 Machine Learning이 Optimization과의 distinct 한 차이를 보여줌.
Optimization은 목적 자체가 objective funtion을 하는 것.
Machine Learning은 unseen data까지도 파악 하고자 하는 것.
3. Curvature커브를 추가함으로써 Optimization을 돕는 것. ( 그래프에서 쫙 올라가는게 아닌 커브를 주는 부분 표현)

W2는 무게감을 spread out 값을 펴냄. 쫙 Flat하게 해서 비교한다는 걸로 보면 좋을 듯.
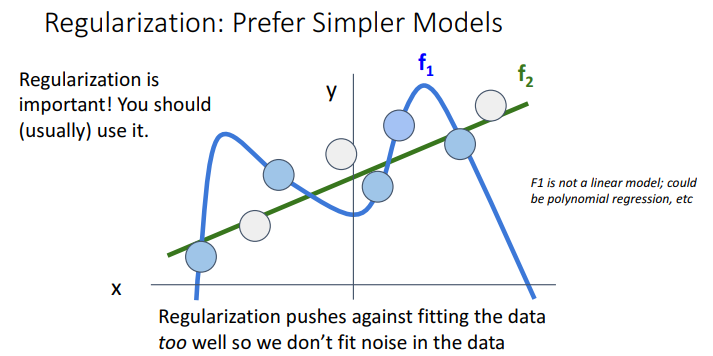
Regularization은 간단한 값을 좋아하기 때문에 f2값을 좋아함. (f1은 여기서 linear model이 아닌 polynomial regression 임)
Regularization은 중요함!!
머신러닝할 때 자주 사용하여야함.

Cross-Entropy Loss (Multinomial Logistic Regression)은
위와 같은 -log 함수를 통해서 Maximum Likelihood Estimation을 만들어 낸다.
즉, choose weights (무게감을 늘림으로써), 가능성을 가장 크게 만들어 예측을 하는 것.


위의 Kullback-Leibler Divergence 와 Cross Entropy는 위의 두 값들을 비교하는데 사용됨

Cross-Entropy Loss 의 경우
1. s= f(Xi; W)
2. Softmax funtion 사용
3. 마이너스 로그로 확률을 최대화
4. 마지막으로 Kullback Leibler로 모두 함께 넣어준다 (comparing하여 select?)


CIFAR10 사용하는 경우 2.3 정도를 봐야함.
여기 부분 잘 이해 안됨..



마지막 정리..
Linear Classfier에서 값을 보는 3가지 View point
1. Algebraic viewpoint
2. Visual Viewpoint
3. Geometric Viewpoint 를 배움

구해진 데이터들 중에 선호도를 나타내기 위한 Loss Function
1. Linear Classifier로 값을 구하고 Loss funtion (Softmax, SVM, Full Loss)로 data loss 손실량을 구해서 선호도 파악
2. 이 후 값들 중에서 가장 좋은 값을 찾기 위해 Regularization을 활용 by spreading out the data.

다음 시간엔 Optimization 할 차례..
정신 줄 놓지 말자!! 화이팅!!
'CS231 Summary & 마음대로 해석' 카테고리의 다른 글
| CS231 Lecture 7: Convolutional Networks (0) | 2021.02.07 |
|---|---|
| CS231 Lecture 5: Backpropagation (0) | 2021.01.31 |
| CS231 Lecture 5: Neural Networks (0) | 2021.01.24 |
| CS231 Lecture 4: Optimization (0) | 2021.01.17 |
| CS231 Lec.02 Image Classification (0) | 2021.01.04 |